This extended example shows how function return values and local definitions can work together to express general ideas concisely. We will implement an algorithm that is used broadly in machine learning, scientific computing, hardware design, and optimization.

Newton's method is a classic iterative approach to finding the arguments of a mathematical function that yield a return value of 0. These values are called the zeros of the function. Finding a zero of a function is often equivalent to solving some other problem of interest, such as computing a square root.

A motivating comment before we proceed: it is easy to take for granted the fact that we know how to compute square roots. Not just Python, but your phone, web browser, or pocket calculator can do so for you. However, part of learning computer science is understanding how quantities like these can be computed, and the general approach presented here is applicable to solving a large class of equations beyond those built into Python.

Newton's method is an iterative improvement algorithm: it improves a guess of the zero for any function that is differentiable, which means that it can be approximated by a straight line at any point. Newton's method follows these linear approximations to find function zeros.

Imagine a line through the point $(x, f(x))$ that has the same slope as the curve for function $f(x)$ at that point. Such a line is called the tangent, and its slope is called the derivative of $f$ at $x$.

This line's slope is the ratio of the change in function value to the change in function argument. Hence, translating $x$ by $f(x)$ divided by the slope will give the argument value at which this tangent line touches 0.

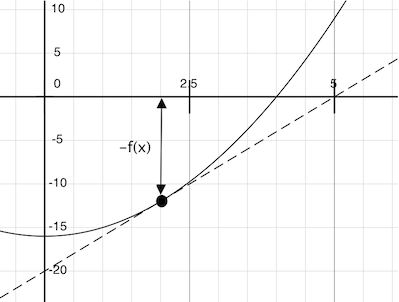
A newton_update expresses the computational process of following this tangent line to 0, for a function f and its derivative df.

>>> def newton_update(f, df):
            def update(x):
                return x - f(x) / df(x)
            return update
    

Finally, we can define the find_root function in terms of newton_update, our improve algorithm, and a comparison to see if $f(x)$ is near 0.

>>> def find_zero(f, df):
            def near_zero(x):
                return approx_eq(f(x), 0)
            return improve(newton_update(f, df), near_zero)
    

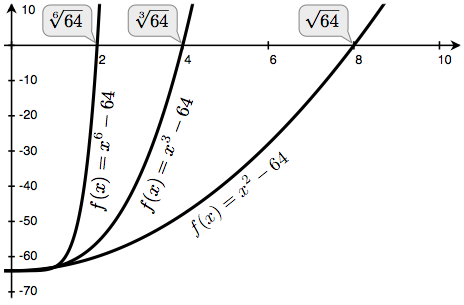
Computing Roots. Using Newton's method, we can compute roots of arbitrary degree $n$. The degree $n$ root of $a$ is $x$ such that $x \cdot x \cdot x \dots x = a$ with $x$ repeated $n$ times. For example,

• The square (second) root of 64 is 8, because $8 \cdot 8 = 64$.
• The cube (third) root of 64 is 4, because $4 \cdot 4 \cdot 4 = 64$.
• The sixth root of 64 is 2, because $2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 64$.

We can compute roots using Newton's method with the following observations:

• The square root of 64 (written $\sqrt{64}$) is the value $x$ such that $x^2 - 64 = 0$
• More generally, the degree $n$ root of $a$ (written $\sqrt[n]{a}$) is the value $x$ such that $x^n - a = 0$

If we can find a zero of this last equation, then we can compute degree $n$ roots. By plotting the curves for $n$ equal to 2, 3, and 6 and $a$ equal to 64, we can visualize this relationship.

We first implement square_root by defining f and its derivative df. We use from calculus the fact that the derivative of $f(x) = x^2 - a$ is the linear function $df(x) = 2x$.

>>> def square_root_newton(a):
            def f(x):
                return x * x - a
            def df(x):
                return 2 * x
            return find_zero(f, df)
    

>>> square_root_newton(64)
    8.0
    

Generalizing to roots of arbitrary degree $n$, we compute $f(x) = x^n - a$ and its derivative $df(x) = n \cdot x^{n-1}$.

>>> def power(x, n):
            """Return x * x * x * ... * x for x repeated n times."""
            product, k = 1, 0
            while k < n:
                product, k = product * x, k + 1
            return product
    

>>> def nth_root_of_a(n, a):
            def f(x):
                return power(x, n) - a
            def df(x):
                return n * power(x, n-1)
            return find_zero(f, df)
    

>>> nth_root_of_a(2, 64)
    8.0
    >>> nth_root_of_a(3, 64)
    4.0
    >>> nth_root_of_a(6, 64)
    2.0
    

The approximation error in all of these computations can be reduced by changing the tolerance in approx_eq to a smaller number.

As you experiment with Newton's method, be aware that it will not always converge. The initial guess of improve must be sufficiently close to the zero, and various conditions about the function must be met. Despite this shortcoming, Newton's method is a powerful general computational method for solving differentiable equations. Very fast algorithms for logarithms and large integer division employ variants of the technique in modern computers.