Consider the following three functions, which all compute summations. The first, sum_naturals, computes the sum of natural numbers up to n:

>>> def sum_naturals(n):
            total, k = 0, 1
            while k <= n:
                total, k = total + k, k + 1
            return total
    

>>> sum_naturals(100)
    5050
    

The second, sum_cubes, computes the sum of the cubes of natural numbers up to n.

>>> def sum_cubes(n):
            total, k = 0, 1
            while k <= n:
                total, k = total + k*k*k, k + 1
            return total
    

>>> sum_cubes(100)
    25502500
    

The third, pi_sum, computes the sum of terms in the series

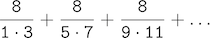
which converges to pi very slowly.

>>> def pi_sum(n):
            total, k = 0, 1
            while k <= n:
                total, k = total + 8 / ((4*k-3) * (4*k-1)), k + 1
            return total
    

>>> pi_sum(100)
    3.1365926848388144
    

These three functions clearly share a common underlying pattern. They are for the most part identical, differing only in name and the function of k used to compute the term to be added. We could generate each of the functions by filling in slots in the same template:

def <name>(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + <term>(k), k + 1
        return total
    

The presence of such a common pattern is strong evidence that there is a useful abstraction waiting to be brought to the surface. Each of these functions is a summation of terms. As program designers, we would like our language to be powerful enough so that we can write a function that expresses the concept of summation itself rather than only functions that compute particular sums. We can do so readily in Python by taking the common template shown above and transforming the "slots" into formal parameters:

In the example below, summation takes as its two arguments the upper bound n together with the function term that computes the kth term. We can use summation just as we would any function, and it expresses summations succinctly. Take the time to step through this example, and notice how binding cube to the local names term ensures that the result 1*1*1 + 2*2*2 + 3*3*3 = 36 is computed correctly. In this example, frames which are no longer needed are removed to save space.

Using an identity function that returns its argument, we can also sum natural numbers using exactly the same summation function.

>>> def summation(n, term):
            total, k = 0, 1
            while k <= n:
                total, k = total + term(k), k + 1
            return total
    

>>> def identity(x):
            return x
    

>>> def sum_naturals(n):
            return summation(n, identity)
    

>>> sum_naturals(10)
    55
    

The summation function can also be called directly, without definining another function for a specific sequence.

>>> summation(10, square)
    385
    

We can define pi_sum using our summation abstraction by defining a function pi_term to compute each term. We pass the argument 1e6, a shorthand for 1 * 10^6 = 1000000, to generate a close approximation to pi.

>>> def pi_term(x):
            return 8 / ((4*x-3) * (4*x-1))
    

>>> def pi_sum(n):
            return summation(n, pi_term)
    

>>> pi_sum(1e6)
    3.141592153589902