Mutable data allows us to simulate systems with change, but also allows us to build new kinds of abstractions. In this extended example, we combine nonlocal assignment, lists, and dictionaries to build a constraint-based system that supports computation in multiple directions. Expressing programs as constraints is a type of declarative programming, in which a programmer declares the structure of a problem to be solved, but abstracts away the details of exactly how the solution to the problem is computed.
Computer programs are traditionally organized as one-directional computations, which perform operations on pre-specified arguments to produce desired outputs. On the other hand, we often want to model systems in terms of relations among quantities. For example, we previously considered the ideal gas law, which relates the pressure (p), volume (v), quantity (n), and temperature (t) of an ideal gas via Boltzmann's constant (k):
p * v = n * k * t
Such an equation is not one-directional. Given any four of the quantities, we can use this equation to compute the fifth. Yet translating the equation into a traditional computer language would force us to choose one of the quantities to be computed in terms of the other four. Thus, a function for computing the pressure could not be used to compute the temperature, even though the computations of both quantities arise from the same equation.
In this section, we sketch the design of a general model of linear relationships. We define primitive constraints that hold between quantities, such as an adder(a, b, c) constraint that enforces the mathematical relationship a + b = c.
We also define a means of combination, so that primitive constraints can be combined to express more complex relations. In this way, our program resembles a programming language. We combine constraints by constructing a network in which constraints are joined by connectors. A connector is an object that "holds" a value and may participate in one or more constraints.
For example, we know that the relationship between Fahrenheit and Celsius temperatures is:
9 * c = 5 * (f - 32)
This equation is a complex constraint between c and f. Such a constraint can be thought of as a network consisting of primitive adder, multiplier, and constant constraints.
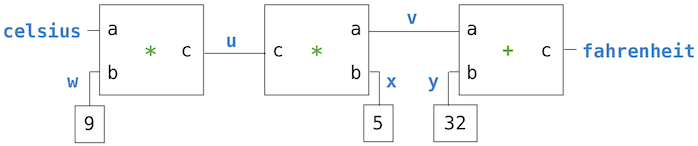
In this figure, we see on the left a multiplier box with three terminals, labeled a, b, and c. These connect the multiplier to the rest of the network as follows: The a terminal is linked to a connector celsius, which will hold the Celsius temperature. The b terminal is linked to a connector w, which is also linked to a constant box that holds 9. The c terminal, which the multiplier box constrains to be the product of a and b, is linked to the c terminal of another multiplier box, whose b is connected to a constant 5 and whose a is connected to one of the terms in the sum constraint.
Computation by such a network proceeds as follows: When a connector is given a value (by the user or by a constraint box to which it is linked), it awakens all of its associated constraints (except for the constraint that just awakened it) to inform them that it has a value. Each awakened constraint box then polls its connectors to see if there is enough information to determine a value for a connector. If so, the box sets that connector, which then awakens all of its associated constraints, and so on. For instance, in conversion between Celsius and Fahrenheit, w, x, and y are immediately set by the constant boxes to 9, 5, and 32, respectively. The connectors awaken the multipliers and the adder, which determine that there is not enough information to proceed. If the user (or some other part of the network) sets the celsius connector to a value (say 25), the leftmost multiplier will be awakened, and it will set u to 25 * 9 = 225. Then u awakens the second multiplier, which sets v to 45, and v awakens the adder, which sets the fahrenheit connector to 77.
Using the Constraint System. To use the constraint system to carry out the temperature computation outlined above, we first create two named connectors, celsius and fahrenheit, by calling the connector constructor.
>>> celsius = connector('Celsius')
>>> fahrenheit = connector('Fahrenheit')
Then, we link these connectors into a network that mirrors the figure above. The function converter assembles the various connectors and constraints in the network.
>>> def converter(c, f):
"""Connect c to f with constraints to convert from Celsius to Fahrenheit."""
u, v, w, x, y = [connector() for _ in range(5)]
multiplier(c, w, u)
multiplier(v, x, u)
adder(v, y, f)
constant(w, 9)
constant(x, 5)
constant(y, 32)
>>> converter(celsius, fahrenheit)
We will use a message passing system to coordinate constraints and connectors. Constraints are dictionaries that do not hold local states themselves. Their responses to messages are non-pure functions that change the connectors that they constrain.
Connectors are dictionaries that hold a current value and respond to messages that manipulate that value. Constraints will not change the value of connectors directly, but instead will do so by sending messages, so that the connector can notify other constraints in response to the change. In this way, a connector represents a number, but also encapsulates connector behavior.
One message we can send to a connector is to set its value. Here, we (the 'user') set the value of celsius to 25.
>>> celsius['set_val']('user', 25)
Celsius = 25
Fahrenheit = 77.0
Not only does the value of celsius change to 25, but its value propagates through the network, and so the value of fahrenheit is changed as well. These changes are printed because we named these two connectors when we constructed them.
Now we can try to set fahrenheit to a new value, say 212.
>>> fahrenheit['set_val']('user', 212)
Contradiction detected: 77.0 vs 212
The connector complains that it has sensed a contradiction: Its value is 77.0, and someone is trying to set it to 212. If we really want to reuse the network with new values, we can tell celsius to forget its old value:
>>> celsius['forget']('user')
Celsius is forgotten
Fahrenheit is forgotten
The connector celsius finds that the user, who set its value originally, is now retracting that value, so celsius agrees to lose its value, and it informs the rest of the network of this fact. This information eventually propagates to fahrenheit, which now finds that it has no reason for continuing to believe that its own value is 77. Thus, it also gives up its value.
Now that fahrenheit has no value, we are free to set it to 212:
>>> fahrenheit['set_val']('user', 212)
Fahrenheit = 212
Celsius = 100.0
This new value, when propagated through the network, forces celsius to have a value of 100. We have used the very same network to compute celsius given fahrenheit and to compute fahrenheit given celsius. This non-directionality of computation is the distinguishing feature of constraint-based systems.
Implementing the Constraint System. As we have seen, connectors are dictionaries that map message names to function and data values. We will implement connectors that respond to the following messages:
- connector['set_val'](source, value) indicates that the source is requesting the connector to set its current value to value.
- connector['has_val']() returns whether the connector already has a value.
- connector['val'] is the current value of the connector.
- connector['forget'](source) tells the connector that the source is requesting it to forget its value.
- connector['connect'](source) tells the connector to participate in a new constraint, the source.
Constraints are also dictionaries, which receive information from connectors by means of two messages:
- constraint['new_val']() indicates that some connector that is connected to the constraint has a new value.
- constraint['forget']() indicates that some connector that is connected to the constraint has forgotten its value.
When constraints receive these messages, they propagate them appropriately to other connectors.
The adder function constructs an adder constraint over three connectors, where the first two must add to the third: a + b = c. To support multidirectional constraint propagation, the adder must also specify that it subtracts a from c to get b and likewise subtracts b from c to get a.
>>> from operator import add, sub
>>> def adder(a, b, c):
"""The constraint that a + b = c."""
return make_ternary_constraint(a, b, c, add, sub, sub)
We would like to implement a generic ternary (three-way) constraint, which uses the three connectors and three functions from adder to create a constraint that accepts new_val and forget messages. The response to messages are local functions, which are placed in a dictionary called constraint.
>>> def make_ternary_constraint(a, b, c, ab, ca, cb):
"""The constraint that ab(a,b)=c and ca(c,a)=b and cb(c,b) = a."""
def new_value():
av, bv, cv = [connector['has_val']() for connector in (a, b, c)]
if av and bv:
c['set_val'](constraint, ab(a['val'], b['val']))
elif av and cv:
b['set_val'](constraint, ca(c['val'], a['val']))
elif bv and cv:
a['set_val'](constraint, cb(c['val'], b['val']))
def forget_value():
for connector in (a, b, c):
connector['forget'](constraint)
constraint = {'new_val': new_value, 'forget': forget_value}
for connector in (a, b, c):
connector['connect'](constraint)
return constraint
The dictionary called constraint is a dispatch dictionary, but also the constraint object itself. It responds to the two messages that constraints receive, but is also passed as the source argument in calls to its connectors.
The constraint's local function new_value is called whenever the constraint is informed that one of its connectors has a value. This function first checks to see if both a and b have values. If so, it tells c to set its value to the return value of function ab, which is add in the case of an adder. The constraint passes itself (constraint) as the source argument of the connector, which is the adder object. If a and b do not both have values, then the constraint checks a and c, and so on.
If the constraint is informed that one of its connectors has forgotten its value, it requests that all of its connectors now forget their values. (Only those values that were set by this constraint are actually lost.)
A multiplier is very similar to an adder.
>>> from operator import mul, truediv
>>> def multiplier(a, b, c):
"""The constraint that a * b = c."""
return make_ternary_constraint(a, b, c, mul, truediv, truediv)
A constant is a constraint as well, but one that is never sent any messages, because it involves only a single connector that it sets on construction.
>>> def constant(connector, value):
"""The constraint that connector = value."""
constraint = {}
connector['set_val'](constraint, value)
return constraint
These three constraints are sufficient to implement our temperature conversion network.
Representing connectors. A connector is represented as a dictionary that contains a value, but also has response functions with local state. The connector must track the informant that gave it its current value, and a list of constraints in which it participates.
The constructor connector has local functions for setting and forgetting values, which are the responses to messages from constraints.
>>> def connector(name=None):
"""A connector between constraints."""
informant = None
constraints = []
def set_value(source, value):
nonlocal informant
val = connector['val']
if val is None:
informant, connector['val'] = source, value
if name is not None:
print(name, '=', value)
inform_all_except(source, 'new_val', constraints)
else:
if val != value:
print('Contradiction detected:', val, 'vs', value)
def forget_value(source):
nonlocal informant
if informant == source:
informant, connector['val'] = None, None
if name is not None:
print(name, 'is forgotten')
inform_all_except(source, 'forget', constraints)
connector = {'val': None,
'set_val': set_value,
'forget': forget_value,
'has_val': lambda: connector['val'] is not None,
'connect': lambda source: constraints.append(source)}
return connector
A connector is again a dispatch dictionary for the five messages used by constraints to communicate with connectors. Four responses are functions, and the final response is the value itself.
The local function set_value is called when there is a request to set the connector's value. If the connector does not currently have a value, it will set its value and remember as informant the source constraint that requested the value to be set. Then the connector will notify all of its participating constraints except the constraint that requested the value to be set. This is accomplished using the following iterative function.
>>> def inform_all_except(source, message, constraints):
"""Inform all constraints of the message, except source."""
for c in constraints:
if c != source:
c[message]()
If a connector is asked to forget its value, it calls the local function forget-value, which first checks to make sure that the request is coming from the same constraint that set the value originally. If so, the connector informs its associated constraints about the loss of the value.
The response to the message has_val indicates whether the connector has a value. The response to the message connect adds the source constraint to the list of constraints.
The constraint program we have designed introduces many ideas that will appear again in object-oriented programming. Constraints and connectors are both abstractions that are manipulated through messages. When the value of a connector is changed, it is changed via a message that not only changes the value, but validates it (checking the source) and propagates its effects (informing other constraints). In fact, we will use a similar architecture of dictionaries with string-valued keys and functional values to implement an object-oriented system later in this chapter.